Task — Zero array

You are given an array of non-negative integers, @ints. Write a script to return the minimum number of operations to make every element equal zero.

In each operation, you are required to pick a positive number less than or equal to the smallest element in the array, then subtract that from each positive element in the array.

Examples

Example 1:
Input: @ints = (1, 5, 0, 3, 5)
Output: 3

operation 1: pick 1 => (0, 4, 0, 2, 4)
operation 2: pick 2 => (0, 2, 0, 0, 2)
operation 3: pick 2 => (0, 0, 0, 0, 0)

Example 2:
Input: @ints = (0)
Output: 0

Example 3:
Input: @ints = (2, 1, 4, 0, 3)
Output: 4

operation 1: pick 1 => (1, 0, 3, 0, 2)
operation 2: pick 1 => (0, 0, 2, 0, 1)
operation 3: pick 1 => (0, 0, 1, 0, 0)
operation 4: pick 1 => (0, 0, 0, 0, 0)

Analysis

At first glance this looks like another challenge requiring recursion, or an equivalent stacking algorithm.

However, I postulate, and think I can demonstrate, that by picking the smallest remaining non-zero element in @ints for each operation, the number of operations cannot be bettered.

The statement of the challenge allows one to pick a number which is less than the smallest remaining element, but I believe that will never result in fewer operations (although it may provide an alternative way of achieving the same number).

Here, briefly, is my logic. First, the order of the elements of @ints clearly doesn't affect the answer, so let's sort them in increasing order, and represent them as a series of stacked blocks:

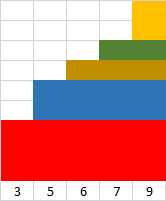
My hypothesis says that each operation removes the blocks of a single colour, starting from red and moving up. The red block is 3 high, because I'm not allowed to exceed 3, the smallest non-zero element in \@ints. Repeatedly doing this means I remove blocks of the same colour in each operation, requiring 5 operations to clear them all.

Now suppose that I decide to pick 2 instead of 3 as my first operation.

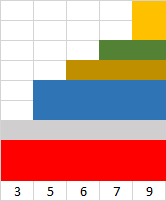
You can see that that will not clear the leftmost column, and I will need to make a second pick of 1 to remove the row of grey blocks - and it can only be 1 because the leftmost column only contains 1 block after I've removed the red blocks. And the result is that I will now need 6 operations.

So no recursion is needed: simply repeatedly pick the smallest remaining item in @ints.

Prove me wrong - with an example - if you can!

Try it 

Script

#!/usr/bin/perl

use v5.16;    # The Weekly Challenge - 2023-07-17
use utf8;     # Week 226 task 2 - Zero array
use strict;   # Peter Campbell Smith
use warnings; # Blog: http://ccgi.campbellsmiths.force9.co.uk/challenge

my ($j, @ints);

zero_array(1, 5, 0, 3, 5);
zero_array(2, 1, 4, 0, 3);

for $j (0 .. 20) {
    push @ints, int(rand(20));
}
zero_array(@ints);

sub zero_array {
    
    my (@ints, @sorted, $j, $count, $least, $explain);
    
    @ints = @_;
    say qq[\nInput:  \@ints = (] . join(', ', @ints) . qq[)];
    $count = 0;
    $explain = '';

    while (1) {
        
        # find the least non-zero element left
        @sorted = sort { $a <=> $b } @ints;
        shift @sorted while (@sorted and $sorted[0] == 0);
        last unless @sorted;
        $least = $sorted[0];
        
        # subtract least from all non-zeroes
        for $j (0 .. @ints - 1) {
            $ints[$j] -= $least if $ints[$j];
        }
        $count ++;
        $explain .= qq[operation $count: pick $least => (] . join(', ', @ints) . qq[)\n];
    }
    $explain =~ s|\n$||;
    say qq[Output: $count\n$explain];

}

Output

Input:  @ints = (1, 5, 0, 3, 5)
Output: 3
operation 1: pick 1 => (0, 4, 0, 2, 4)
operation 2: pick 2 => (0, 2, 0, 0, 2)
operation 3: pick 2 => (0, 0, 0, 0, 0)

Input:  @ints = (2, 1, 4, 0, 3)
Output: 4
operation 1: pick 1 => (1, 0, 3, 0, 2)
operation 2: pick 1 => (0, 0, 2, 0, 1)
operation 3: pick 1 => (0, 0, 1, 0, 0)
operation 4: pick 1 => (0, 0, 0, 0, 0)

Input:  @ints = (3, 0, 18, 10, 15, 0, 18, 18, 9, 11, 5, 17, 17, 7, 14, 12, 3, 18, 17, 14, 10)
Output: 11
operation 1: pick 3 => (0, 0, 15, 7, 12, 0, 15, 15, 6, 8, 2, 14, 14, 4, 11, 9, 0, 15, 14, 11, 7)
operation 2: pick 2 => (0, 0, 13, 5, 10, 0, 13, 13, 4, 6, 0, 12, 12, 2, 9, 7, 0, 13, 12, 9, 5)
operation 3: pick 2 => (0, 0, 11, 3, 8, 0, 11, 11, 2, 4, 0, 10, 10, 0, 7, 5, 0, 11, 10, 7, 3)
operation 4: pick 2 => (0, 0, 9, 1, 6, 0, 9, 9, 0, 2, 0, 8, 8, 0, 5, 3, 0, 9, 8, 5, 1)
operation 5: pick 1 => (0, 0, 8, 0, 5, 0, 8, 8, 0, 1, 0, 7, 7, 0, 4, 2, 0, 8, 7, 4, 0)
operation 6: pick 1 => (0, 0, 7, 0, 4, 0, 7, 7, 0, 0, 0, 6, 6, 0, 3, 1, 0, 7, 6, 3, 0)
operation 7: pick 1 => (0, 0, 6, 0, 3, 0, 6, 6, 0, 0, 0, 5, 5, 0, 2, 0, 0, 6, 5, 2, 0)
operation 8: pick 2 => (0, 0, 4, 0, 1, 0, 4, 4, 0, 0, 0, 3, 3, 0, 0, 0, 0, 4, 3, 0, 0)
operation 9: pick 1 => (0, 0, 3, 0, 0, 0, 3, 3, 0, 0, 0, 2, 2, 0, 0, 0, 0, 3, 2, 0, 0)
operation 10: pick 2 => (0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0)
operation 11: pick 1 => (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)