
Peter Campbell Smith
Anyone for chess?
Weekly challenge 281 — 5 August 2024
Week 281: 5 Aug 2024
Task — Knight’s move
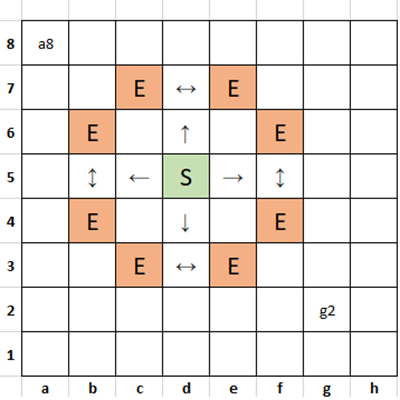
A Knight in chess can move from its current position to any square two rows or columns plus one column or row away. So in the diagram below, if it starts at S, it can move to any of the squares marked E.
Write a script which takes a starting position and an ending position and calculates the least number of moves required.
Examples
Example 1 Input: $start = 'g2', $end = 'a8' Output: 4 g2 -> e3 -> d5 -> c7 -> a8 Example 2 Input: $start = 'g2', $end = 'h2' Output: 3 g2 -> e3 -> f1 -> h2
Analysis
I submitted this challenge, but had no preconceived idea as to how it might be solved.
If you ask a chess player to solve it, he or she will glance at the board and give you the answer. But it isn't that easy to calculate.
I considered a number of possible approaches. My first thought was a recursive search, generating all possible paths from the starting square and seeing which reached the target square first. But a quick calculation suggested that there would be a lot of paths, so I went for a different strategy.
My solution finds all the squares which are one move from the start square, and then all the ones that are 2 moves away and so on until one of the found squares is the target square. The number of moves taken to get there will be the minimum possible, because all shorter paths have already been shown not to reach the target.
In generating the moves it is necessary to discard a move to a square which has already been visited, and of course to discard ones that fall off the edge of the chessboard. This greatly reduces the number of paths under consideration at any point in the process.
In order to generate the printout of the path I save the predecessor of each endpoint and then work back from the final target.
I wondered whether it was necessary to allow for a case where the end square was unreachable, but I convinced myself that the knight can reach any square from any other square, and I could not find any example where more than 6 moves are needed.
One decision I had to make was whether to identify squares internally by their chess name - a1 to h8 - or to work with x and y coordinates. I tried both, and decided that working with the chess names led to clearer code.
Try it
Script
#!/usr/bin/perl # Blog: http://ccgi.campbellsmiths.force9.co.uk/challenge use v5.26; # The Weekly Challenge - 2024-08-05 use utf8; # Week 281 - task 2 - Knight's move use warnings; # Peter Campbell Smith binmode STDOUT, ':utf8'; knights_move('g2', 'a8'); knights_move('g2', 'h2'); knights_move('a1', 'h8'); knights_move('e3', 'e4'); sub knights_move { my (@valid_moves, $from_square, $to_square, %from, $moves, $square, $v, $trace, $square2, $x, $y, $s, %m, $next_square); # x, y changes for valid moves @valid_moves = ([-2, 1], [-1, 2], [1, 2], [2, 1], [-2, -1], [-1, -2], [1, -2], [2, -1]); # initialise $from_square = $_[0]; $to_square = $_[1]; say qq[\nInput: \$start = '$from_square', \$end = '$to_square']; for $x ('a' .. 'h') { for $y (1 .. 8) { $from{$x . $y} = ''; $m{$x . $y} = -1; } } $from{$from_square} = 0; $m{$from_square} = 0; # find squares $moves away from starting square for $moves (1 .. 10) { # look at every square for $s (0 .. 63) { # select those accessible in $moves - 1 moves $square = chr(ord('a') + $s % 8) . (int($s / 8) + 1); if ($m{$square} == $moves - 1) { # mark squares accessible from them for $v (@valid_moves) { $next_square = displace($square, $v); next if $next_square eq 'invalid'; next unless $from{$next_square} eq ''; # we've arrived! if ($next_square eq $to_square) { $trace = $to_square; $square2 = $square; while (1) { $trace = $square2 . qq[ → $trace]; last if $square2 eq $from_square; $square2 = $from{$square2}; } say qq[Output: $moves ($trace)]; return; } $from{$next_square} = $square; $m{$next_square} = $moves; } } } } } sub displace { my (@square, $x, $y); # displace($square, $x, $y) returns square displaced by those increments ($x, $y) = $_[0] =~ m|(.)(.)|; @square = @{$_[1]}; $x = chr(ord($x) + $square[0]); $y = $y + $square[1]; return ($x lt 'a' or $x gt 'h' or $y < 1 or $y > 8) ? 'invalid' : $x . $y; }
Output
Input: $start = 'g2', $end = 'a8' Output: 4 (g2 → e3 → c4 → b6 → a8) Input: $start = 'g2', $end = 'h2' Output: 3 (g2 → e3 → f1 → h2) Input: $start = 'a1', $end = 'h8' Output: 6 (a1 → b3 → c1 → e2 → f4 → g6 → h8) Input: $start = 'e3', $end = 'e4' Output: 3 (e3 → f1 → d2 → e4)
Any content of this website which has been created by Peter Campbell Smith is in the public domain