Task — Rectangle area

You are given coordinates bottom-left and top-right corner of two rectangles in a 2D plane. Write a script to find the total area covered by the two rectangles.

Examples

Example 1:
Input: Rectangle 1 => (-1,0), (2,2)
       Rectangle 2 => (0,-1), (4,4)
Output: 22

Example 2:
Input: Rectangle 1 => (-3,-1), (1,3)
       Rectangle 2 => (-1,-3), (2,2)
Output: 25

Analysis

Mohammad and Colin like it when the task is slightly under-defined, but I took it that the area we are looking for is the area covered by one or both rectangles. If the rectangles don't overlap then clearly it's just the sum of the two rectangles' areas, but if they do overlap we then have to subtract the overlapped area, as we've counted it twice.

There are a lot of possibilities for overlap, such as:

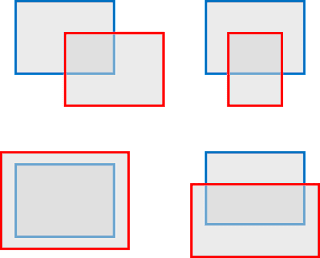
But do they overlap?

Condition 1: The rectangles may overlap if the bottom of rect1 is below the top of rect2 and the top of rect1 is above the bottom of rect2.

Condition 2: They may also overlap if the right of rect1 is to the right of the left of rect2 and the left of rect1 is to the left of the right side of rect2.

They do overlap if condition 1 and condition 2 are both true, or else they don't.

So now we need the area of the overlap. The overlap area is bounded by:

• the greater of the bottoms,
• the lesser of the tops,
• the leftmost of the rights and
• the rightmost of the lefts.

If that sounds complicated, apply it to the examples shown above and you'll see what I mean.

This works for 2 rectangles, but if there are 3 or more it gets harder, but I won't tell you how to do that in case it's next week's challenge.

Try it 

Try running the script with any input:

Your @rect1 = ([bottom left x, y], [top right x, y])

example: [0, 1], [2, 3]

Your @rect2 = ([bottom left x, y], [top right x, y])

example: [1, 2], [3, 4]

⤡

#!/usr/bin/perl

# Peter Campbell Smith - 2022-02-17
# PWC 152 task 2

use v5.28;
use strict;
use utf8;

my ($example, $area, $horiz_overlap, $vert_overlap, %rect);

for $example (1 .. 4) {
    
    # input
    if ($example == 1) {
        #         rect    bottom   left     top     right
        %rect = ( one => {b => -1, l =>  0, t => 2, r => 2},
                  two => {b =>  0, l => -1, t => 4, r => 4} );
                  
    } elsif ($example == 2) {
        %rect = ( one => {b => -3, l => -1, t => 1, r => 3},
                  two => {b => -1, l => -3, t => 2, r => 2} );

    } elsif ($example == 3) {   # rect2 wholly within rect1
        %rect = ( one => {b => -2, l => -2, t => 2, r => 2},
                  two => {b => -1, l => -1, t => 1, r => 1} );
                  
    } elsif ($example == 4) {   # no overlap
        %rect = ( one => {b => 0, l => 0, t => 2, r => 2},
                  two => {b => 2, l => 2, t => 4, r => 4} );
    }
    
    say qq[\nInput:  Rectangle 1 => ($rect{one}{b}, $rect{one}{l}), ($rect{one}{t}, $rect{one}{r})
    Rectangle 2 => ($rect{two}{b}, $rect{two}{l}), ($rect{two}{t}, $rect{two}{r})];
             
    # Assume no overlap for now
    $area = area('one') + area('two');
                  
    # The rectangles may overlap if the bottom of rect1 is below the top of rect2
    # and the top of rect1 is above the bottom of rect2
    $vert_overlap = $rect{one}{b} < $rect{two}{t} && $rect{one}{t} > $rect{two}{b};

    # They may also overlap if the right of rect1 is to the right of the left of rect2
    # and the left of rect1 is to the left of the right side of rect2
    $horiz_overlap = $rect{one}{r} > $rect{two}{l} && $rect{one}{l} < $rect{two}{r};

    # They do overlap if both of these conditions are true
    if ($vert_overlap && $horiz_overlap) {
        
        # ... and the overlap area is bounded by the greater of the bottoms,
        # the lesser of the tops, the leftmost of the rights and the rightmost 
        # of the lefts      
        $rect{overlap}{b} = $rect{one}{b} > $rect{two}{b} ? $rect{one}{b} : $rect{two}{b};
        $rect{overlap}{t} = $rect{one}{t} > $rect{two}{t} ? $rect{two}{t} : $rect{one}{t};
        $rect{overlap}{l} = $rect{one}{l} > $rect{two}{l} ? $rect{one}{l} : $rect{two}{l};
        $rect{overlap}{r} = $rect{one}{r} > $rect{two}{r} ? $rect{two}{r} : $rect{one}{r};
        
        $area -= area('overlap');
    } else {
        say qq[   No overlap];
    }
    
    say qq[Output: $area];
}

sub area {
    
    my $this = shift;
    my $area = ($rect{$this}{t} - $rect{$this}{b}) * ($rect{$this}{r} - $rect{$this}{l});
    say qq[   Area of $this is $area];
    return $area;
}

Output

Input:  Rectangle 1 => (-1, 0), (2, 2)
	Rectangle 2 => (0, -1), (4, 4)
   Area of one is 6
   Area of two is 20
   Area of overlap is 4
Output: 22

Input:  Rectangle 1 => (-3, -1), (1, 3)
	Rectangle 2 => (-1, -3), (2, 2)
   Area of one is 16
   Area of two is 15
   Area of overlap is 6
Output: 25

Input:  Rectangle 1 => (-2, -2), (2, 2)
	Rectangle 2 => (-1, -1), (1, 1)
   Area of one is 16
   Area of two is 4
   Area of overlap is 4
Output: 16

Input:  Rectangle 1 => (0, 0), (2, 2)
	Rectangle 2 => (2, 2), (4, 4)
   Area of one is 4
   Area of two is 4
   No overlap
Output: 8