Task — Cardano triplets

Write a script to generate first 5 Cardano Triplets. A triplet of positive integers (a,b,c) is called a Cardano Triplet if it satisfies this condition: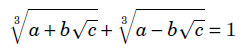

Examples

Example 1:
(2, 1, 5) is the first Cardano Triplet.

Analysis

Exactly how you order the triplets and thus determine which are the first 5 is not specified, but I took it to mean the first 5 if you order them by a + b + c.

I chose to do this by testing all possible triplets containing numbers up to 100, of which there are 1 million. By iterating first over c, then b, then a I saved a little time by calculating sqrt(c) only 100 times, and b * sqrt(c) only 10 000 times, but in fact that made little difference: my little Raspberry Pi did it in under 5 seconds with or without my optimisation (maybe because Perl does it anyway).

If we write the definition of the triplets in the form t1 + t2 = 1 it is interesting to look at the pattern. In every case t1 is >1 and t2 is thus negative, for example:

triplet (32, 11, 85) yields 5.10977222864644 + 
   -4.10977222864644 = 1

There are some sets of triplets where their the t1 of each and thus the t2 of each are the same, for example:

(47, 40, 20)  → 6.09016994374947 + -5.09016994374947 = 1
(47, 80, 5)   → 6.09016994374947 + -5.09016994374947 = 1
(47, 20, 80)  → 6.09016994374947 + -5.09016994374947 = 1
(47, 16, 125) → 6.09016994374947 + -5.09016994374947 = 1

By inspection, it appears that there is only one (t1, t2) pair for a given a: that is, any triplets where a is, for example, 47, will have the same t1 and t2. That implies that they also share b * sqrt(c) and thus b**2 * c, and indeed from the 47 example:

b = 40, c= 20   so b**2 * c = 1600 * 20 = 32000
b = 80, c = 5   so b**2 * c = 6400 * 5  = 32000
b = 20, c = 80  so b**2 * c = 400 * 80  = 32000
b = 16, c = 125 so b**2 * c = 256 * 125 = 32000

From that pattern we can deduce that the following are also Cardano triplets:

(47, 10, 320) and (47, 5, 1280)
(47, 8, 500), (47, 4, 2000), (47, 2, 8000) 
   and (47, 1, 32000)

To get those I took the original set of 47s and successively divided b by 2 and multiplied c by 4 until b was indivisible by 2 (with an integral result), and similarly multiplied b by 2 and divided c by 4 until c was indivisible.

Can we then say that we have identified all the triplets where a = 47? I postulate that this is the case.

It must be the case that any factor of 32000 that is a square will generate at least one triplet. The prime factors of 32000 are 2**8 * 5**3. So the possible square factors of 32000, ie the possible b**2s, are:

1, 4, 16, 64, 256, 25, 100, 400, 1600, 6400

... and thus the possible values of b are:

1, 2, 4, 8, 16, 5, 10, 20, 40 and 80

... and all of these are in the original set (for which I only searched a, b, and c up to 100), or in the 6 others that I deduced.

But remember that I postulated that all triplets with a = 47 have the same t1 and t2. I can't prove that, although the evidence suggests that it is the case.

So could we do the same for, say a = 48? At this point I can't see (a) how we could do that, or (b) prove whether in fact any triplets exist for a = 48, but I leave that - as one of my textbooks used to say - as an exercise for the reader.

⤡

#!/usr/bin/perl

# Peter Campbell Smith - 2022-01-10
# PWC 148 task 2

use v5.28;
use warnings;
use strict;
use utf8;

my ($a, $b, $c, $sqrt_c, %results, $cardano, $sum, $answer, $term1, $term2, $j, $b_sqrt_c);

# try 1 million possibilities - probably overkill!
for $c (1 .. 100) {
    $sqrt_c = sqrt($c);
    for $b (1 .. 100) {
        $b_sqrt_c = $b * $sqrt_c;
        for $a (1 .. 100) {
            
            # need to allow for imprecision in floating point operations
            $term1 = cbrt($a + $b_sqrt_c);
            $term2 = cbrt($a - $b_sqrt_c);
            if (abs($term1 + $term2 - 1) < 1e-10) {
                $results{sprintf('%06d¦%s', $a + $b + $c, 
                    qq[$a, $b, $c :: $term1 + $term2 = 1])} = 1;
            }   
        }
    }
}
    
# sort and print results in ascending order of a + b + c
$j = 0;
say qq[\nFirst 5 Cardano triplets];
for $cardano (sort keys %results) {
    ($sum, $answer) = split('¦', $cardano);
    say $answer;
    say qq[\n... and some more] if ++$j == 5;
}

sub cbrt {
    
    # cube root
    my $arg = $_[0];
    if ($arg >= 0) {
        return $arg ** (1 / 3);
        
    # cube root of -x is minus cube root of x
    } else {
        return -((-$arg) ** (1 / 3));
    }
}

Output

First 5 Cardano triplets
2, 1, 5 :: 1.61803398874989 + -0.618033988749895 = 1
5, 2, 13 :: 2.30277563773199 + -1.30277563773199 = 1
8, 3, 21 :: 2.79128784747792 + -1.79128784747792 = 1
17, 18, 5 :: 3.85410196624968 + -2.85410196624968 = 1
11, 4, 29 :: 3.19258240356725 + -2.19258240356725 = 1

... and some more
17, 9, 20 :: 3.85410196624968 + -2.85410196624968 = 1
14, 5, 37 :: 3.54138126514911 + -2.54138126514911 = 1
5, 1, 52 :: 2.30277563773199 + -1.30277563773199 = 1
17, 6, 45 :: 3.85410196624968 + -2.85410196624968 = 1
20, 7, 53 :: 4.14005494464026 + -3.14005494464026 = 1
23, 8, 61 :: 4.40512483795333 + -3.40512483795333 = 1
44, 45, 13 :: 5.90832691319598 + -4.90832691319598 = 1
26, 9, 69 :: 4.65331193145904 + -3.65331193145904 = 1
47, 40, 20 :: 6.09016994374947 + -5.09016994374947 = 1
29, 10, 77 :: 4.88748219369606 + -3.88748219369606 = 1
32, 11, 85 :: 5.10977222864644 + -4.10977222864644 = 1
47, 80, 5 :: 6.09016994374947 + -5.09016994374947 = 1
35, 12, 93 :: 5.32182538049648 + -4.32182538049648 = 1
47, 20, 80 :: 6.09016994374947 + -5.09016994374947 = 1
71, 72, 21 :: 7.37386354243376 + -6.37386354243376 = 1
71, 36, 84 :: 7.37386354243376 + -6.37386354243376 = 1
98, 99, 29 :: 8.57774721070176 + -7.57774721070176 = 1